Researchers have developed a novel approach to pricing American options, a type of financial derivative, by combining fractional calculus and deep learning techniques. The study, published in the journal Scientific Reports, explores how the integration of these two powerful tools can yield more accurate and realistic predictions of option prices, particularly in complex financial markets. Derivatives are financial instruments whose value is derived from the performance of an underlying asset, such as stocks, bonds, or commodities. American options, in particular, can be exercised at any time before the expiration date, making them more flexible and attractive to investors compared to European options, which can only be exercised at the expiration date.
Fractional Calculus and the Complexity of Financial Markets
Conventional models for pricing American options, such as the calculus’>fractional calculus, which uses non-integer order derivatives. By incorporating fractional derivatives, the researchers developed a generalized Black-Scholes model that can better account for the long-range memory and non-stationary nature of financial time series.
Combining Fractional Calculus and Neural Networks
To solve the free boundary problem associated with American options, the researchers employed a combined physics-informed neural network (CPINN). This approach combines the power of fractional calculus with the flexibility of deep learning, allowing the model to learn the underlying physical constraints of the problem while also adapting to the unique characteristics of the financial market data.
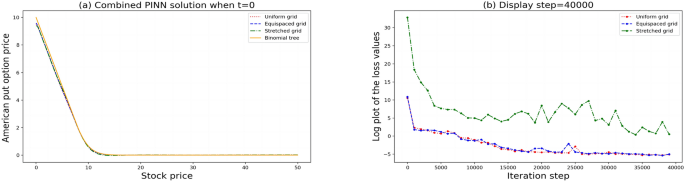
The CPINN is designed to approximate the parameters of the generalized Black-Scholes model, including the unknown free boundary, which represents the optimal exercise price for the American option. The researchers introduced a solution assumption and a data enhancement layer to improve the accuracy and convergence of the neural network algorithm.
Exploring Different Fractional Derivatives
The study explores the performance of the CPINN under three different fractional derivative definitions: Caputo, Caputo-Fabrizio, and Atangana-Baleanu-Caputo fractional derivatives. These non-local fractional derivatives can better capture the complex behavior of financial markets compared to the classical integer-order derivatives.

The researchers found that the CPINN algorithm performed well in predicting American put option prices under all three fractional derivative models, demonstrating the flexibility and effectiveness of the approach. Importantly, the choice of fractional derivative order had a relatively small impact on the overall price trends, but did affect the numerical values, highlighting the importance of capturing the subtle differences in market dynamics.
Real-World Applications and Future Directions
To validate the practical relevance of their approach, the researchers tested the CPINN on real market data for an American put option, and compared its performance to a direct application of the neural network method proposed by Wang and Perdikaris. The results showed that the CPINN had lower prediction errors, indicating its potential for real-world applications.

The study also simulated the optimal exercise boundary for American put options under the different fractional derivative models, providing valuable insights for investors and market makers. The researchers emphasize that the combination of fractional calculus and neural networks offers a promising avenue for further research in option pricing and other financial applications.
Broader Implications and Future Directions
The successful integration of fractional calculus and deep learning techniques in this study has broader implications for the scientific community. The researchers suggest that the approach can be extended to study free boundary problems in other research fields, such as physics and engineering, where complex systems and non-local phenomena play a significant role.
Moreover, the researchers highlight the potential for further improvements, such as enhancing the predictive accuracy and stability of the models, expanding the application to a wider range of option types and financial markets, and exploring more advanced machine learning algorithms. As artificial intelligence and computational power continue to advance, the synergy between fractional calculus and neural networks is poised to unlock new frontiers in the understanding and modeling of complex systems.

Author credit: This article is based on research by Lina Song, Yousheng Tan, Fajun Yu, Yangcheng Luo, Jingjing Zheng.
For More Related Articles Click Here
