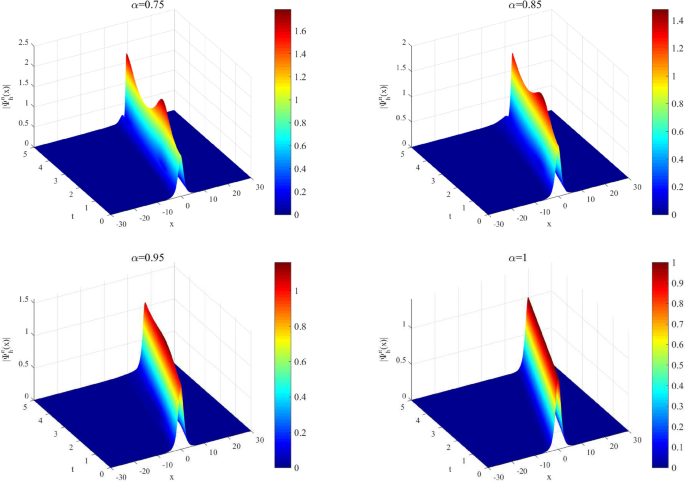
Researchers have developed a new computational method to solve complex nonlinear partial differential equations known as the space-fractional Schrödinger equation. This equation is used to model the behavior of quantum mechanical waves, with applications in fields like nonlinear optics and atomic physics. The new split-step finite element method avoids complex iterations, preserves key mathematical properties, and can efficiently simulate wave dynamics in two dimensions. This breakthrough could lead to improved modeling of quantum phenomena and the development of advanced photonic devices.
Modeling Complex Quantum Waves
The standard calculus’>fractional derivatives in space. These fractional derivatives can better represent the non-local and anomalous diffusion behavior observed in some quantum systems, such as superconductors and optics’>nonlinear optics and Click Here
</b>.</p>
<p>The key idea behind the split-step FEM is to divide the original problem into two simpler subproblems: a linear subproblem and a nonlinear subproblem. By solving these subproblems sequentially, the method avoids the need for complex iterations at each time step, significantly reducing the computational cost.</p>
<figure class="wp-block-image size-large"><img decoding="async" src="https://famefreq.s3.us-east-2.amazonaws.com/1729079644_41598_2024_75547_Fig2_HTML.png" alt="figure 2" style="width: 100%; height: auto;" /><figcaption class="wp-element-caption">Fig. 2</figcaption></figure>
<p><h3>Preserving Key Mathematical Properties</h3>
</p>
<p>In addition to its computational efficiency, the split-step FEM developed by the researchers has other important properties:</p>
<p>– <strong>Mass Conservation<strong>: The method preserves the <b>mass conservation law</b>, ensuring that the phase and shape of the simulated waves are maintained over long time periods.<br />
– <strong>Convergence<strong>: The researchers have proven that the split-step FEM converges to the exact solution with a desired order of accuracy, both in time and space.</p>
<p>These mathematical properties are crucial for accurately modeling the dynamics of quantum waves, which is essential for applications in fields like nonlinear optics and atomic physics.</p>
<p><h3>Simulating Two-Dimensional Wave Dynamics</h3>
</p>
<p>The researchers demonstrated the effectiveness of their split-step FEM by applying it to solve the two-dimensional space-fractional Schrödinger equation. They conducted several numerical examples, including simulating the propagation of solitons (localized wave solutions) and the dynamics of defocusing waves.</p>
<p>The results showed that the fractional power, <b>α</b>, significantly affects the shape and behavior of the simulated waves. As the fractional power decreases, the wave solutions become more localized and travel more slowly, highlighting the importance of using the space-fractional Schrödinger equation to accurately model complex quantum phenomena.</p>
<p><h3>Advancing Quantum Modeling and Applications</h3>
</p>
<p>The development of the split-step finite element method for the space-fractional Schrödinger equation represents a significant advancement in the field of computational quantum mechanics. By combining the efficiency of split-step techniques with the versatility of the finite element method, the researchers have created a powerful tool for simulating the dynamics of quantum waves in two dimensions.</p>
<p>This work could lead to improved modeling of quantum phenomena and the development of advanced photonic devices, such as those used in <a href=){kind=link}