Researchers have developed a groundbreaking quantum error correction method using ‘many-hypercube codes’ that boasts an elegant geometric structure, potentially paving the way for highly efficient and fault-tolerant quantum computing.
A Fault-Tolerant Approach to Fully Unlocked Quantum Computing
Quantum computers have the potential to transform many industries, from cryptography and materials science to drug discovery. On the other hand, the delicacy of quantum systems results in a big challenge in creating a type of quantum computing that is reliable and scalable.
In order to address this challenge, researchers have been investigating novel quantum error correction techniques. In a remarkable study that appeared this week in the journal Science Advances, Hayato Goto from RIKEN Center for Quantum Computing (Japan) presented an alternative novel method based on ‘many-hypercube codes’ with a nice albeit complicated geometry disrupting germane notions of error correcting codes as previously known and aimed to supply avenues to profound practical benefits in efficient corrections of errors feasibly used toward building fault-tolerant quantum computing.
Goto added “We have hope that the construction of large-scale quantum computers — fault-tolerant ones, which are capable of correcting errors mid-calculation and able to surpass classical computers for a few tasks — will be possible within our lifetimes, thanks to the experimental progress in recent years. This is where efficient quantum error correction will come in, but how do we develop one?
Geometric elegance transforming the art of quantum error correction
The standard quantum error correction strategy generally encodes a single logical qubit (the quantum counterpart of a classical bit) onto several connected physical qubits before recovering the logical qubit with a decoder. Although this is an approach that has been explored quite extensively, it is limited by its scalability as the need for physical qubits grows exponentially which in turn leads to a very high resource overhead.
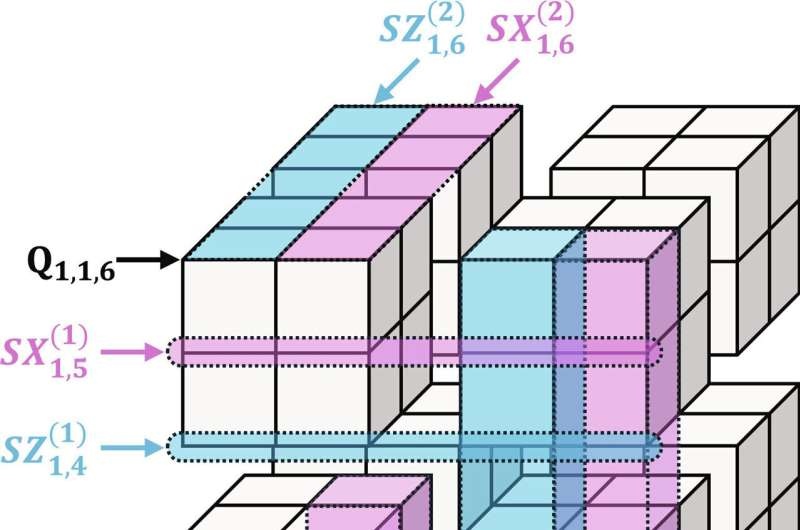
To that end, Goto and his team proposed an interesting method called ‘many-hypercube codes. Alternatively, in mathematical terms this family of codes can be seen as representing a ‘hypercube’ — a geometric figure built from squares and cubes but also generalizing to higher-dimensional shapes like the tesseract.
Perhaps even more remarkable about these “many-hypercube codes” is that they have an unusually simple structure, by the standards of high rate quantum codes; most such codes tend to be convoluted. A key motivation for their work here is the elegant geometry of these codes, which might allow profound advances in fault-tolerant quantum computing. Goto recalls
What sets the many-hypercube codes of Goto’s team apart from other methods is that it allows logical gates to be laid out concurrently, rather than in series. The notion that code can be executed in parallel (read: independently) is similar to the concept of ‘high-performance computing’ made possible by multiple cores in a CPU and Goto calls this ‘high-performance fault-tolerant computing’ which I believe has a ring to it.
Conclusion
The creation of the ‘many-hypercube codes’ by Hayato Goto (pictured) and colleagues at the RIKEN Center for Quantum Computing could signal a step towards practical quantum computing. The elegance and the ability of parallelized logical gates are making these codes potential frontrunners for a new era of quantum computing, which could be both highly scalable and reliable. In the world of quantum technology research, advances like this will prove vital in meeting the challenge of topological qubit based quantum error correction and realizing the capacity for computation that early visionaries believed could be possible.
